الفرق بين المستطيل و المعين: المستطيل مقابل المعين

المستطيل مقابل المعين

المعين والمستطيل هي الرباعية. عرفت هندسة هذه الأرقام للإنسان لآلاف السنين. يتم التعامل مع هذا الموضوع بشكل واضح في كتاب "عناصر" كتبه عالم الرياضيات اليوناني يوكليد.

متوازي الأضلاع

يمكن تعريف متوازي الأضلاع بالشكل الهندسي مع أربعة جوانب، مع موازاة الجانبين معا. على وجه التحديد هو رباعي مع اثنين من أزواج من الجانبين المتوازيين. هذه الطبيعة الموازية تعطي العديد من الخصائص الهندسية لمتوازي الأضلاع.

A رباعي الأضلاع هو متوازي الأضلاع إذا تم العثور على الخصائص الهندسية.

• زوجان من الجانبين المتعارضين متساوون في الطول. (أب = دس، أد = بك)

• زوجان من الزوايا المتعارضة متساويان في الحجم. (

)

• إذا كانت الزوايا المجاورة تكميلية

• زوج من الجانبين، التي تعارض بعضها البعض، موازية ومتساوية في الطول. (أب = دس & أبدك)

• تقسم الأقطار بعضها البعض (أو = أوك، بو = أود)

• يقسم كل قطري الرباعي إلى مثيلتين متطابقتين. (ΔADB ≡ ΔBCD، ΔABC ≡ ΔADC)

وعلاوة على ذلك، مجموع مربعات الجانبين يساوي مجموع مربعات الأقطار. ويشار إلى هذا أحيانا باسم قانون متوازي الاضلاع ولديه تطبيقات واسعة في الفيزياء والهندسة. (أب ² + بك ² + سد ² + دا ² = أس ² + بد < 2 ⁾ كل من الخصائص المذكورة أعلاه يمكن أن تستخدم كخصائص، مرة واحدة ثبت أن الرباعي هو متوازي الأضلاع.

يمكن حساب مساحة متوازي الأضلاع بواسطة نتاج طول جانب واحد والارتفاع إلى الجانب الآخر. لذلك، يمكن تحديد منطقة متوازي الأضلاع

مساحة متوازي الاضلاع = قاعدة × ارتفاع =

أب × h منطقة متوازي الاضلاع مستقلة عن شكل متوازي الأضلاع الفردية. وهي تعتمد فقط على طول القاعدة وارتفاع عمودي.

إذا كان يمكن تمثيل جانبي متوازي الأضلاع بناقلات اثنين، يمكن الحصول على المنطقة من خلال حجم المنتج المتجه (المنتج المتقاطع) للناقلين المتجاورين.

إذا تم تمثيل الجانبين أب و أد من قبل المتجهات () و (

) على التوالي، يتم إعطاء منطقة متوازي الأضلاع

، حيث α هي الزاوية بين

و.

فيما يلي بعض خصائص متقدمة من متوازي الاضلاع.

• منطقة متوازي الأضلاع هي ضعف مساحة المثلث التي تم إنشاؤها بواسطة أي من الأقطار.

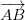
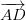
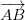
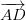
• تنقسم مساحة متوازي الأضلاع إلى النصف بواسطة أي خط يمر عبر النقطة الوسطى.

• أي تحول أفيني غير متحول يأخذ متوازي الأضلاع إلى متوازي الاضلاع آخر

• متوازي الأضلاع لديه التناظر التناوب من النظام 2

• مجموع المسافات من أي نقطة داخلية متوازي الأضلاع إلى الجانبين مستقلة عن موقع النقطة

المستطيل

ويعرف الرباعي مع أربعة زوايا قائمة كمستطيل. هو حالة خاصة من متوازي الاضلاع حيث الزوايا بين أي الجانبين المتاخمة هي زوايا قائمة.

بالإضافة إلى جميع خصائص متوازي الأضلاع، يمكن التعرف على خصائص إضافية عند النظر في هندسة المستطيل.

• كل زاوية في القمم هي زاوية صحيحة.

• أقطار متساوية في الطول، وأنها تشطر بعضها البعض. ولذلك، فإن المقاطع المتقطعة هي أيضا متساوية في الطول.

• يمكن حساب طول الأقطار باستخدام نظرية فيثاغورس:

يا

2

+ بس ² = سك ² يقلل إلى نتاج الطول والعرض. ^{مساحة المستطيل = الطول × العرض}

• توجد العديد من الخصائص المتماثلة على مستطيل، مثل؛

- المستطيل هو دوري، حيث يمكن وضع جميع القمم على محيط الدائرة.

- إنها متساوية، حيث كل الزوايا متساوية.

- هو إيسوغونال، حيث تقع جميع الزوايا داخل مدار التناظر نفسه.

- له التناظر العاكسي والتناظر التناوبي.

المعين

A الرباعية مع جميع الأطراف متساوية في طول يعرف باسم المعين. ويسمى أيضا باسم

رباعي الأضلاع متساوية الأضلاع

. ويعتبر أن يكون شكل الماس، على غرار واحد في أوراق اللعب. المعين هو أيضا حالة خاصة من متوازي الاضلاع. ويمكن اعتباره متوازي الأضلاع مع جميع الجوانب الأربعة متساوية. ولها خصائص خاصة التالية، بالإضافة إلى خصائص متوازي الاضلاع. • أقطار المعين تشترك بعضها البعض في زوايا قائمة؛ الأقطار متعامدة.

• تقطع الأقطار الزوايا الداخلية المقابلة.

• على الأقل اثنين من الجانبين المتاخمة متساوية في الطول.

يمكن حساب منطقة المعين بنفس طريقة متوازي الأضلاع.

ما هو الفرق بين المعين والمستطيل؟

• المعين والمستطيل هي الرباعية. المستطيل و المعين هي حالات خاصة من متوازي الاضلاع.

• يمكن حساب أي منطقة باستخدام الصيغة

قاعدة × ارتفاع

. • النظر في الأقطار؛ - أقطار المعين تقسم بعضها البعض في زوايا قائمة، والمثلثات شكلت متساوية الأضلاع.

- أقطار المستطيل متساوية في الطول وتشطر بعضها البعض. المقاطع المقطوعة متساوية في الطول. الأقطار تقسم المستطيل إلى اثنين من المثلثات الصحيحة متطابقة.

• النظر في الزوايا الداخلية.

- الزوايا الداخلية للمعين مقطوعة من الأقطار

- جميع الزوايا الداخلية الأربعة للمستطيل هي زوايا قائمة.

• النظر في الجانبين.

- بما أن جميع الجوانب الأربعة متساوية في المعين، أربعة أضعاف مربع من الجانب يساوي مجموع مربعات قطري (باستخدام قانون متوازي الأضلاع)

- في المستطيلات، ومجموع المربعات من الجانبين المتاخمين يساوي مربع قطري في نهايات.(قاعدة فيثاغورس)