الفرق بين سلسلة باور وسلسلة تايلور
سلسلة الطاقة مقابل سلسلة تايلور
في الرياضيات، تسلسل حقيقي هو قائمة مرتبة من الأرقام الحقيقية. رسميا، بل هو وظيفة من مجموعة من الأرقام الطبيعية في لمجموعة من الأرقام الحقيقية. إذا كان a n هو مدة تسلسل، فإننا نشير إلى التسلسل من خلال 1 أو a 2 ، …، a n، …. على سبيل المثال، ضع في الاعتبار التسلسل 1، ½، ⅓، …، 1 / n ، …. يمكن أن يشار إليه على أنه {1 / n}.
من الممكن تحديد سلسلة باستخدام تسلسل. سلسلة هي مجموع شروط تسلسل. لذلك، لكل تسلسل، هناك تسلسل المرتبطة والعكس بالعكس. إذا كان {a n} هو التسلسل قيد النظر، فإن السلسلة التي تم تشكيلها بواسطة هذا التسلسل يمكن تمثيلها على النحو التالي:
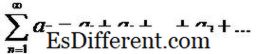
وهكذا، في المثال السابق، تكون السلسلة المرتبطة 1+ 1 / 2 + 1 / 3 + … + 1 / n + ….
وكما تشير الأسماء، فإن سلسلة الطاقة هي نوع خاص من السلسلة، وهي تستخدم على نطاق واسع في التحليل العددي والنمذجة الرياضية ذات الصلة. سلسلة تايلور هي سلسلة السلطة الخاصة التي توفر وسيلة بديلة وسهلة للتلاعب لتمثيل وظائف معروفة.
ما هي سلسلة الطاقة؟
سلسلة الطاقة هي سلسلة من الاستمارة

التي تكون متقاربة (ربما) لبعض الفواصل التي تركز على ج. يمكن أن تكون المعاملات a n أرقام حقيقية أو معقدة، وتكون مستقلة عن x؛ أنا. ه. المتغير الوهمية.
على سبيل المثال، من خلال تعيين a n = 1 لكل n، و c = 0، سلسلة الطاقة 1 + x + x 2 + … + x n + … يتم الحصول عليها. فمن السهل أن نلاحظ أنه عندما س ε (-1، 1)، هذه السلسلة السلطة يتقارب إلى 1 / (1-س).
تتقارب سلسلة الطاقة عند x = c. القيم الأخرى x التي تتلاقى سلسلة الطاقة دائما تأخذ شكل فاصل مفتوح مركز على c. هذا هو ، سيكون هناك قيمة 0≤ R ذلك أن كل x تلبية | شك | ≤ R ، سلسلة الطاقة متقاربة ولكل x مرضية | شك>> R ، سلسلة الطاقة متباينة. وتسمى هذه القيمة R نصف قطر تقارب سلسلة الطاقة (R يمكن أن تأخذ أي قيمة حقيقية أو إنفينيتي إيجابية).


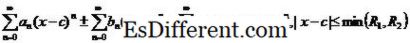
يتم إضافة عبارات مماثلة أو طرحها معا. أيضا، فمن الممكن مضاعفة وقسمة سلسلة السلطة اثنين باستخدام الهوية، ما هو سلسلة تايلور؟

يتم تعريف سلسلة تايلور لوظيفة
f (x) التي تختلف بشكل لا نهائي عن الفاصل الزمني. افترض أن f (x) تختلف على فاصل زمني مركز على c. ثم سلسلة السلطة التي تعطى

f (x) حول c. & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ & نبسب؛ ج). في التحليل العددي، يتم استخدام عدد محدود من المصطلحات في هذا التوسع اللانهائي في حساب القيم عند النقاط التي تكون فيها السلسلة متقاربة مع الوظيفة الأصلية. و (x ) يقال أن تكون تحليلية في الفاصل الزمني (أ، ب)، إذا كان لكل x ε (أ، ب)، سلسلة تايلور f (x) تتلاقى مع الدالة f (x). على سبيل المثال، 1 / (1-x) تحليلي على (-1، 1)، منذ توسع تايلور 1 + x + x 2 + … + x n + … كونفيرجيس (999




