الفرق بين التكامل والتجميد: التكامل مقابل التجمعات مقارنة

التكامل مقابل التلخيص

في الرياضيات الثانوية العليا، التكامل والتجميع غالبا ما توجد في العمليات الرياضية. ويبدو أنها تستخدم كأدوات مختلفة وفي حالات مختلفة، لكنها تشترك في علاقة وثيقة جدا.

المزيد عن الملخص

الملخص هو عملية إضافة سلسلة من الأرقام وغالبا ما يشار إلى العملية بالحرف اليوناني لرأس المال سيغما Σ. يتم استخدامه لاختصار الجمع ويساوي مجموع / مجموع تسلسل. وغالبا ما تستخدم لتمثيل هذه السلسلة، والتي هي أساسا متواليات لانهائية لخص. ويمكن أيضا أن تستخدم للإشارة إلى مجموع النواقل، المصفوفات، أو متعددو الحدود.

يتم الجمع عادة لمجموعة من القيم التي يمكن تمثيلها بواسطة مصطلح عام، مثل السلسلة التي لها مصطلح مشترك. وتعرف نقطة الانطلاق ونقطة النهاية بالحد الأدنى والحد الأعلى للجمع، على التوالي.

على سبيل المثال، مجموع تسلسل ₁ ، ₂ ، ₃ ، ₄ ، … _n هو ₁ + a ₂ + a ₃ + … + a _n باستخدام الرمز التجميعي Σ ⁿ _{i = 1} a _i ؛ i يسمى مؤشر الجمع.

وتستخدم العديد من الاختلافات لجمع استنادا إلى التطبيق. في بعض الحالات، يمكن إعطاء الحد الأعلى والحد الأدنى كفاصل زمني أو نطاق، مثل Σ _1≤i≤100 a _i و _{i [1، 100]} a _i . أو يمكن أن تعطى كمجموعة من الأرقام مثل Σ _إيب a _i ، حيث P هي مجموعة محددة.

في بعض الحالات، يمكن استخدام اثنين أو أكثر من علامات سيغما، ولكن يمكن تعميمها على النحو التالي؛ Σ _j Σ _k a _جك = Σ _{j، k} a _جك .

أيضا، يتبع الجمع العديد من القواعد الجبرية. وبما أن العملية جزءا لا يتجزأ من إضافة، العديد من القواعد المشتركة للجبر يمكن تطبيقها على المبالغ نفسها وبالنسبة للمصطلحات الفردية التي يصورها الجمع.

المزيد عن التكامل

يعرف التكامل بأنه عملية التمايز العكسي. ولكن في نظرتها الهندسية يمكن أيضا أن تعتبر المنطقة المغلقة من قبل منحنى وظيفة والمحور. ولذلك، فإن حساب المنطقة يعطي قيمة التكامل التام كما هو موضح في الرسم البياني.

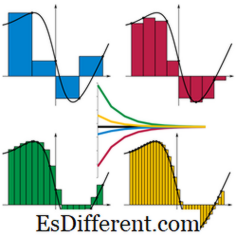
إيماج سورس: هتب: // أر. ويكيبيديا. أورغ / ويكي / ملف: Riemann_sum_convergence. بابوا نيو غينيا

قيمة التكامل المحدد هي في الواقع مجموع الشرائط الصغيرة داخل المنحنى والمحور.منطقة كل شريط هو الطول × العرض عند نقطة على محور النظر. العرض هو قيمة يمكننا أن نختار، ويقول Δx. والارتفاع هو تقريبا قيمة الدالة عند النقطة المحددة، f (x _i ). من الرسم البياني، فمن الواضح أن أصغر الشرائط هي أفضل شرائط تناسب داخل المنطقة المحصورة، وبالتالي أفضل تقريبي للقيمة.

لذلك، بشكل عام، التكامل التام I بين النقاط a و b (i e في الفاصل الزمني [a، b] حيث 1 ) Δx + f (x ₂ ) Δx + ⋯ + f n _{) Δx، حيث n هو عدد الشرائط (n = (با) / Δx) ويمكن تمثيل هذا الجمع للمنطقة بسهولة باستخدام تدوين التجمعات ك} I ≅ Σ < n i = 1 ^f _(x i) Δx وحيث أن التقريب يكون أفضل عندما يكون Δx أصغر، يمكننا حساب القيمة عند Δx → 0 ولذلك، من المعقول القول _I = ليم Δx → 0 Σ _n i = 1 ^f ) Δx كالتعميم من المفهوم أعلاه، يمكننا أن نختار Δx على أساس الفاصل الزمني المفهرس المفهرسة من قبل (اختيار عرض المنطقة على أساس الموقف)، ثم نحصل على < I _{= ليم} Δx → 0

Δx → 0

n _{i = 1} f ^{> i} ₌ a ∫ _b f _{(x) دكس} هذا ما يعرف باسم ريمان إنتغرال أوف ذي _f (x) في الفاصل الزمني [a، b]. وفي هذه الحالة تعرف a و b باسم الحد الأعلى والحد الأدنى من التكامل. ريمان التكامل هو شكل أساسي من جميع أساليب التكامل. ^{في جوهرها، والتكامل هو جمع المنطقة عندما يكون عرض المستطيل غير محدود.} ما هو الفرق بين التكامل والتجمع؟ • الجمع هو إضافة سلسلة من الأرقام. عادة ما يتم جمعها في هذا النموذج Σ

n i = 1 a

i

عندما يكون المصطلح في التسلسل له نمط ويمكن التعبير عنه باستخدام مصطلح عام.

• التكامل هو في الأساس المنطقة التي يحدها منحنى وظيفة، والمحور والحدود العليا والسفلى. ويمكن إعطاء هذه المنطقة كمجموع مناطق أصغر بكثير في المنطقة المحصورة. ^{• يتضمن التلخيص القيم المنفصلة مع الحدود العليا والسفلى، في حين يتضمن التكامل القيم المستمرة.} _{• يمكن تفسير التكامل على أنه شكل خاص من أشكال الجمع.} • في أساليب الحساب العددي، يتم تنفيذ التكامل دائما كمجموعة.