الفرق بين الأرقام العقلانية وغير العقلانية الفرق بين

يشير مصطلح "الأرقام" إلى ما يتم تصنيفه عموما على أنه قيم صحيحة موجبة أكبر من الصفر. وتشمل الفئات الأخرى من الأرقام أرقام كاملة و أرقام ، مجمع و أرقام حقيقية وأيضا قيم صحيحة سالبة .

توسيع تصنيفات الأرقام بشكل أكبر، نواجه عقلانية و أرقام غير عقلانية . العدد المنطقي هو رقم يمكن كتابته ككسر. وبعبارة أخرى، يمكن كتابة العدد الرشيد كنسبة من رقمين.

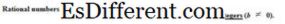
فكر، على سبيل المثال، رقم 6 . ويمكن أن تكون مكتوبة كنسبة من رقمين بمعنى. 6 و 1 ، مما يؤدي إلى نسبة 6/1 . وبالمثل، 2/3 ، وهو مكتوب ككسر، هو رقم عقلاني.

يمكننا، بالتالي، تحديد عدد عقلاني، كعدد مكتوب في شكل جزء، حيث يكون كل من البسط (العدد على القمة) والمقام (العدد في الأسفل) أرقام كاملة. وبالتعريف، فإن كل رقم كامل هو أيضا رقم عقلاني.

نسبة عددين كبيرين مثل ( 129، 367، 871 ) / ( 547، 724، 863 سيشكل أيضا مثالا لرقم عقلاني لسبب بسيط هو أن البسط والمقام هما أرقام كاملة.

وعلى العكس من ذلك، فإن أي رقم لا يمكن التعبير عنه في شكل جزء أو نسبة يسمى بأنه غير عقلاني. المثال الأكثر شيوعا هو رقم غير عقلاني هو √ 2 ( 1. 414213 …) . مثال شعبي آخر على عدد غير عقلاني هو ثابت رقمي π ( 3. 141592 … ) .

يمكن كتابة عدد غير عقلاني كعشرية، ولكن ليس ككسر. لا يتم استخدام الأرقام غير الرشيد في الحياة اليومية على الرغم من أنها موجودة على خط الرقم. هناك عدد لا حصر له من الأرقام غير المنطقية بين 0 و 1 على سطر الأرقام. يحتوي عدد غير عقلاني على أرقام غير متكررة لا نهاية لها على يمين النقطة العشرية.

لاحظ أن القيمة المستشهد بها 22/7 ثابتة π هي في الواقع قيمة واحدة فقط من π >. وبحكم التعريف، فإن محيط الدائرة مقسوما على نصف قطرها هو قيمة π. يؤدي هذا إلى قيم متعددة π ، بما في ذلك، على سبيل المثال لا الحصر، 333/106، 355/113 وهكذا 1. فقط جذور مربع من أرقام مربع. أنا. ه. ، جذور مربع

المربعات الكمال هي عقلانية. -

√1

= 1 (عقلاني) √2

(غير عقلاني) √3

(غير عقلاني) √4 < = 2

(عقلانية) √5، √6، √7، √8 (غير عقلاني)

√9 = 3

(راتيونال) وهلم جرا. وعلاوة على ذلك، نلاحظ أن فقط n

جذور n ث القوى عقلانية. وبالتالي، فإن 6 جذر 64 عقلاني، لأن 64 هي 6 ، وهي 6 قوة 2 . ولكن 6th جذر 63 غير منطقي. 63 ليست مثالية 6 عشر السلطة.

لا محالة، فإن التمثيل العشري لل إراتيونالز يأتي في الصورة ويطرح بعض النتائج المثيرة للاهتمام.

عندما نعبر عن

عقلاني

رقم كعشرية، فإن العشرية ستكون بالضبط (كما في 1/5 = 0. 20) أو قد يكون إنكساكت (كما في 1/3 ≈ 0. 3333 ). في كلتا الحالتين، سيكون هناك نمط يمكن التنبؤ به من الأرقام. لاحظ أنه عندما يتم التعبير عن غير عقلاني رقم عشري، فمن الواضح أنه سيكون غير دقيق، لأنه بخلاف ذلك، فإن العدد سيكون منطقيا. وعلاوة على ذلك، لن يكون هناك نمط يمكن التنبؤ به من الأرقام. على سبيل المثال، √2 ≈

1. 4142135623730950488016887242097

الآن، مع أرقام عقلانية، نواجه أحيانا 1/11 = 0. 0909090

. يعني استخدام كل من علامة المساواة ( =) وثلاث نقاط ( الحذف ) أنه على الرغم من أنه من غير الممكن التعبير عن 1/11 بالضبط كعشرية، لا يزال بإمكاننا تقريبها مع العديد من الأرقام العشرية كما يسمح بالاقتراب من 1/11 . وهكذا، فإن الشكل العشري من 1/11

يعتبر غير دقيق. وبنفس الطريقة، يكون الشكل العشري ¼ وهو 0. 25، بالضبط. القادمة إلى الشكل العشري للأرقام غير الرشيد، فإنها ستكون دائما غير دقيقة. مع الاستمرار في مثال √

2 ، عندما نكتب √2 = 1. 41421356237 … (لاحظ استخدام الحذف)، يعني على الفور أنه لا يوجد عشري ل > √2 سيكون دقيقا. وعلاوة على ذلك، لن يكون هناك نمط يمكن التنبؤ به من الأرقام. باستخدام المفاهيم من الأساليب العددية، مرة أخرى، يمكننا تقريب منطقيا لكثير من الأرقام العشرية حتى هذه النقطة أننا قريبون من √2 . لا يمكن أن تنتهي أي ملاحظة بشأن الأرقام العقلانية وغير المنطقية دون إثبات إلزامي على السبب في أن √2 غير عقلاني. في القيام بذلك، ونحن أيضا توضيح، والمثال الكلاسيكي من برهان من قبل كونت راديكتيون.

لنفترض أن √2 عقلاني. وهذا يقودنا إلى تمثيله كنسبة من اثنين من الأعداد الصحيحة، ويقول p

و

q . √2 = p / q وغني عن القول، p

و

ف ليس لديهم عوامل مشتركة، إذا كان هناك أي عوامل مشتركة، لهم من البسط والمقام. تربيع كلا الجانبين من المعادلة، ونحن في نهاية المطاف مع، - 2

/ q

2

يمكن أن يكون هذا مكتوب بشكل ملائم، p 2 = 2q > 2

تشير المعادلة الأخيرة إلى أن

p 2 حتى. هذا ممكن فقط إذا p

في حد ذاته هو حتى. وهذا يعني ضمنا أن p 2 قابلة للقسمة بواسطة 4 . وبالتالي، يجب أن يكون q 2 وبالتالي q حتى.حتى p و q على حد سواء حتى وهو ما يتناقض مع افتراضنا الأولي أنه ليس لديهم عوامل مشتركة. وبالتالي، √2 لا يمكن أن يكون عقلانيا. Q. E. D.