الفرق بين متوازي أضلاع والرباعي: متوازي أضلاع مقابل الرباعي

متوازي الاضلاع مقابل الرباعي < رباعية الأضلاع ومتوازي الاضلاع هي المضلعات الموجودة في الهندسة الإقليدية. متوازي الأضلاع هو حالة خاصة من الرباعية. كوادريلاتيرالس يمكن أن يكون إما مستو (2D) أو 3 الأبعاد في حين متوازي الاضلاع دائما مستو.

الرباعية

الرباعي هو مضلع مع أربعة جوانب. لديها أربع رؤوس، ومجموع الزوايا الداخلية هي 3600 (2π راد). تصنف كوادريلاتيرالز إلى فئات رباعية متقاطعة ذاتيا وبسيطة. أما الرباعي الرباعي المتقاطع ذاتيا، فيعبر جانبان أو أكثر عن بعضهما البعض، وتتشكل الأشكال الهندسية الأصغر حجما (مثل المثلثات داخل الرباعي).

وتنقسم كوادريلاتيرالس بسيطة أيضا إلى كوادريلاتيرال محدبة ومقعرة. كوادريلاتيرالس مقعرة لها الجانبين المتجاورة تشكيل زوايا منعكس داخل الشكل. كوادريلاتيرالس بسيطة التي ليس لها زوايا منعكس داخليا هي كوادريلاتيرال محدبة. يمكن أن يكون رباعي الأرضيات محدبة دائما تيسلاتيونس.

جزء رئيسي من هندسة الرباعي في المستويات الأولية يتعلق بالحدود الرباعية المحدبة. بعض الرباعية هي مألوفة جدا لنا من أيام المدارس الابتدائية. وفيما يلي رسم تخطيطي يوضح رباعي أضلاع محدبة.

متوازي الأضلاع

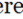
يمكن تعريف متوازي الأضلاع بالشكل الهندسي مع أربعة جوانب، مع وجود جانبي متقابلين موازين لبعضهما البعض. على وجه التحديد هو رباعي مع اثنين من أزواج من الجانبين المتوازيين. هذه الطبيعة الموازية تعطي العديد من الخصائص الهندسية لمتوازي الأضلاع.

A رباعي الأضلاع هو متوازي الأضلاع إذا تم العثور على الخصائص الهندسية التالية.

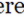
• زوجان من الجانبين المتعارضين متساوون في الطول. (أب = دس، أد = بك)

• زوجان من الزوايا المتعارضة متساويان في الحجم. <>

إذا كانت الزوايا المجاورة تكميلية

• يكون زوج من الجانبين، اللذين يعارضان بعضهما البعض، متوازيين ومتوازيين في الطول. (أب = دس & أبدك)

• أقطار الأقطار بعضها البعض (أو = أوك، بو = أود)

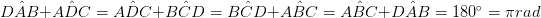
• كل قطري يقسم الرباعي إلى اثنين من المثلثات متطابقة. (ΔADB ≡ ΔBCD، ΔABC ≡ ΔADC)

وعلاوة على ذلك، مجموع مربعات الجانبين يساوي مجموع مربعات الأقطار. ويشار إلى هذا أحيانا باسم

قانون متوازي الاضلاع

ولديه تطبيقات واسعة في الفيزياء والهندسة. (أب 2 + بك ² + سد ² + دا ² = أس ² + بد < 2 ⁾ كل من الخصائص المذكورة أعلاه يمكن أن تستخدم كخصائص، مرة واحدة ثبت أن الرباعي هو متوازي الأضلاع. ^{يمكن حساب مساحة متوازي الأضلاع بواسطة نتاج طول جانب واحد والارتفاع إلى الجانب الآخر. لذلك، يمكن تحديد منطقة متوازي الأضلاع} مساحة متوازي الاضلاع = قاعدة × ارتفاع =

أب

×

h منطقة متوازي الاضلاع مستقلة عن شكل متوازي الأضلاع الفردية. وهي تعتمد فقط على طول القاعدة وارتفاع عمودي. إذا كان يمكن تمثيل جانبي متوازي الأضلاع بناقلات اثنين، يمكن الحصول على المنطقة من خلال حجم المنتج المتجه (المنتج المتقاطع) للناقلين المتجاورين. إذا تم تمثيل الجانبين أب و أد من قبل المتجهات (

) و () على التوالي، يتم إعطاء منطقة متوازي الأضلاع

، حيث α هي الزاوية بين

و.

فيما يلي بعض خصائص متقدمة من متوازي الاضلاع.

• منطقة متوازي الأضلاع هي ضعف مساحة المثلث التي تم إنشاؤها بواسطة أي من الأقطار.

• تنقسم مساحة متوازي الأضلاع إلى النصف بواسطة أي خط يمر عبر النقطة الوسطى.

• أي تحول أفيني غير متحول يأخذ متوازي الأضلاع إلى متوازي الاضلاع آخر

• متوازي الأضلاع لديه التناظر التناوب من النظام 2

• مجموع المسافات من أي نقطة داخلية متوازي الأضلاع إلى الجانبين مستقلة عن موقع النقطة

ما هو الفرق بين متوازي الاضلاع و رباعي؟

• كوادريلاتيرال هي مضلعات ذات أربعة جوانب (تسمى أحيانا تيتراغونس) بينما متوازي الأضلاع هو نوع خاص من الرباعي.

• يمكن أن يكون للجدران الرباعية جانبيها في طائرات مختلفة (في الفضاء ثلاثي الأبعاد) في حين تقع جميع جوانب متوازي الاضلاع على نفس الطائرة (مستو / 2 الأبعاد).

• يمكن للزوايا الداخلية للرباعية أن تأخذ أي قيمة (بما في ذلك زوايا المنعكس) بحيث تضيف ما يصل إلى 3600. ويمكن أن يكون متوازي الأضلاع فقط زوايا منفرجة كأنواع الحد الأقصى للزاوية.

• أربعة جوانب من الرباعي يمكن أن تكون من أطوال مختلفة في حين أن الجانبين المعاكسين متوازي الاضلاع دائما موازية لبعضها البعض ومساوية في الطول.

أي قطري يقسم متوازي الاضلاع إلى اثنين من المثلثات متطابقة، في حين أن المثلثات التي شكلتها قطري من الرباعية العامة ليست بالضرورة متطابقة.