الفرق بين التمايز والمشتقات

التمايز مقابل مشتق

في التفاضل والتكامل التفاضل والتكامل والمشتقات والتمايز ترتبط ارتباطا وثيقا، ولكنها مختلفة جدا، وتستخدم لتمثيل اثنين الرياضية الهامة المفاهيم المتعلقة بالوظائف.

ما هي المشتقات؟

مشتق الدالة يقيس المعدل الذي تتغير فيه قيمة الدالة مع تغير مدخلاتها. في الدالات متعددة المتغيرات، يعتمد التغيير في قيمة الدالة على اتجاه تغيير قيم المتغيرات المستقلة. ولذلك، في مثل هذه الحالات، يتم اختيار اتجاه معين وتتميز الدالة في هذا الاتجاه بالذات. ويطلق على تلك المشتقة المشتقة الاتجاهية. المشتقات الجزئية هي نوع خاص من المشتقات الاتجاهية.

يمكن تعريف مشتق الدالة المتجهة f بحد أقصى

أينما وجدت بشكل نهائي. كما ذكر من قبل، وهذا يعطينا معدل زيادة وظيفة و على طول اتجاه ناقلات ش. في حالة وظيفة ذات قيمة واحدة، فإن هذا يقلل من التعريف المشتق المعروف بالمشتقات،

على سبيل المثال،

تختلف في كل مكان، والمشتقة تساوي الحد

، وهو ما يساوي

. مشتقات وظائف مثل

موجودة في كل مكان. وهي على التوالي تساوي الوظائف

.

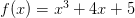
وهذا ما يعرف بالمشتقة الأولى. عادة ما يكون أول مشتق من الدالة f يرمز إليه f ⁽¹⁾ . الآن باستخدام هذا التدوين، فمن الممكن لتحديد المشتقات أعلى النظام.

n ث ^مشتقة f ( ^{n) لكل} n ، ،

n ث ^مشتقة. ما هو التمايز؟

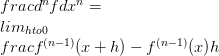
التمايز هو عملية العثور على مشتق من وظيفة مختلفة. D-أوبيراتور "

D يمثل التمايز في بعض السياقات. إذا كان x هو المتغير المستقل، ثم D ≡ d ^/ دكس _{. المشغل D هو مشغل خطي، i. ه. لأي من الدالتين التفاضليتين} f و g وثابت c، بعد الاحتفاظ بالخصائص. I.

d (f < g) = D (f) + D (g) إي

. D سف (سف) < سد (f) باستخدام مشغل D، يمكن التعبير عن القواعد الأخرى المرتبطة بالتمايز على النحو التالي. d (f g) < d (f < ( ^{- _f (g)] / g 2 o g) < D (f) o g _{) D (} g ). على سبيل المثال، عندما تكون F < x = x 2 سين x متباينة فيما يتعلق x باستخدام إن القواعد التي تم تقديمها ستكون الإجابة 2 x سين x - +}

x 2 كوز x . ما هو الفرق بين التمايز ومشتقاته؟ • مشتق يشير إلى معدل تغيير وظيفة • التمايز هو عملية العثور على مشتق من وظيفة.