الفرق بين المشتقات والتفضيلية
مشتق مقابل التفاضلية
في التفاضل والتكامل التفاضل والتكامل، مشتق والتفضيلية وظيفة ترتبط ارتباطا وثيقا ولكن لها معان مختلفة جدا، و تستخدم لتمثيل اثنين من الأشياء الرياضية الهامة ذات الصلة وظائف مختلفة.
ما هي المشتقات؟
مشتق الدالة يقيس المعدل الذي تتغير فيه قيمة الدالة مع تغير مدخلاتها. في الدالات متعددة المتغيرات، يعتمد التغيير في قيمة الدالة على اتجاه تغيير قيم المتغيرات المستقلة. ولذلك، في مثل هذه الحالات، يتم اختيار اتجاه معين وتتميز الدالة في هذا الاتجاه بالذات. ويطلق على تلك المشتقة المشتقة الاتجاهية. المشتقات الجزئية هي نوع خاص من المشتقات الاتجاهية.
يمكن تعريف مشتق الدالة المتجهة f بحد أقصى


على سبيل المثال،





وهذا ما يعرف بالمشتقة الأولى. عادة ما يكون أول مشتق من الدالة f يرمز إليه f (1) . الآن باستخدام هذا التدوين، فمن الممكن لتحديد المشتقات أعلى النظام.
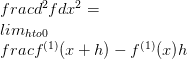

التفاضلية لوظيفة تمثل التغير في الدالة فيما يتعلق بالتغيرات في المتغير المستقل أو المتغيرات. في الدالة المعتادة، بالنسبة إلى وظيفة معينة
f لمتغير واحد x ، يكون الفرق التفاضلي للترتيب 1 دف المعطى بواسطة. وهذا يعني أنه في حالة تغيير غير متناهي الصغر في

x في نقطة تعسفية x و و هو التغيير المطابق في الدالة و. يمكن أن تظهر أن Δ f = f (1) (x ) Δ x + ε، الخطأ. الآن، الحد Δ Δ 0 Δ f / Δ x = f > ( x) (باستخدام التعريف السابق للمشتقات)، وبالتالي، Δ x → 0 ε / Δ x = 0.لذلك، من الممكن أن نستنتج أن Δ x → 0 ε = 0. الآن، تدل Δ x → 0 Δ f d f و x → 0 Δ x كما d x يتم الحصول على تعريف الفرق بدقة. على سبيل المثال، تفاضلية الدالة هي. في حالة وظائف متغيرين أو أكثر، يتم تعريف الفرق الكلي للدالة على أنها مجموع الفوارق في اتجاهات كل من المتغيرات المستقلة. رياضيا، يمكن أن يذكر بأنه.
ما هو الفرق بين المشتقات والتفاضلية؟


، ولكن الفرق هو





