الفرق بين التكاملات المحددة وغير المحددة الفرق بين

حساب التفاضل والتكامل هو فرع مهم من الرياضيات، والتمايز يلعب دورا حاسما في حساب التفاضل والتكامل. ويعرف عملية عكسية من التمايز والتكامل، ويعرف معكوس باسم التكامل، أو ببساطة، وعكس التمايز يعطي متكامل. استنادا إلى النتائج التي تنتج تنقسم تكاملات إلى فئتين بمعنى. ، تكاملات محددة وغير محددة.

محدد إنتغرال

- 1>>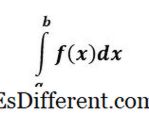

إن التكامل المحدد ل f (x) هو نومبر ويمثل المنطقة تحت المنحنى f (x) من x = a إلى س = ب .

إن التكامل المطلق له حدود علوية وسفلية على التكاملات، ويطلق عليه اسم محدد لأنه، في نهاية المشكلة، لدينا عدد - هو إجابة محددة.

تكاملي غير محدود

إن التكامل غير المحدود ل f (x) هو وظيفة ويجيب على السؤال التالي: "ما هي الوظيفة عندما تعطي متباينة f (x) ؟ "

مع تكامل غير محدود لا توجد حدود أعلى وأدنى على التكامل هنا، وما سنحصل عليه هو الجواب الذي لا يزال لديه x في ذلك وسيكون أيضا ثابت (وعادة ما يشار إليها C ) في ذلك.

عادة ما يعطي التكامل غير المحدود حل عام للمعادلة التفاضلية.

التكامل غير المحدود هو أكثر من شكل عام من التكامل، ويمكن أن تفسر على أنها مكافحة مشتق من وظيفة النظر فيها.

لنفترض أن تمايز الدالة F يؤدي إلى وظيفة أخرى f ، ودمج f يعطي التكامل. رمزيا، يتم كتابة هذا على النحو

F (x) = ∫ƒ (x) دكس

أو

F = ∫ƒ دكس

حيث أن كلا من F و ƒ < هي وظائف x ، و F هي ديفرنتياليابل. في النموذج أعلاه، ويسمى ريمان لا يتجزأ وظيفة الناتجة يرافق ثابت التعسفي. غالبا ما ينتج عن التكامل غير المحدود مجموعة من الوظائف؛ وبالتالي، فإن التكامل هو لأجل غير مسمى.

تكامل وعملية التكامل هي في صميم حل المعادلات التفاضلية. ومع ذلك، خلافا للخطوات في التمايز، خطوات التكامل لا تتبع دائما روتين واضح ومعيار. في بعض الأحيان، نرى أن الحل لا يمكن التعبير صراحة من حيث الوظيفة الابتدائية. وفي هذه الحالة، غالبا ما يعطى الحل التحليلي في شكل تكامل غير محدود.

النظرية الأساسية لحساب التفاضل والتكامل

يتم ربط التكامل المحدد وغير المحدود بالنظرية الأساسية لحساب التفاضل والتكامل على النحو التالي: من أجل حساب

تكامل تام ، ابحث عن تكامل غير محدد > (المعروف أيضا باسم المضاد للمشتقات) للوظيفة ويقيم في النهاية x = a و x = b . سيكون الفرق بين التكاملات المحددة وغير المحددة واضحا عند تقييم التكاملات لنفس الوظيفة. فكر فيما يلي:

موافق. دعونا نفعل كل منهما ونرى الفرق.

للتكامل، نحن بحاجة إلى إضافة واحد إلى الفهرس الذي يقودنا إلى التعبير التالي:

في هذه المرحلة من الزمن

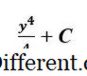
هو مجرد ثابت بالنسبة لنا. هناك حاجة إلى معلومات إضافية في المشكلة لتحديد القيمة الدقيقة C . دعونا نقيم نفس التكامل في شكله المحدد i. ه. ، مع تضمين الحدود العليا والسفلى. <>>>>>

3

بين y = 2 ^و y = 3 >. الخطوة الأولى في هذا التقييم هي نفس التقييم المتكامل إلى أجل غير مسمى. الفرق الوحيد هو أن هذه المرة لا نضيف ثابت C .

التعبير في هذه الحالة يبدو كما يلي: هذا بدوره يؤدي إلى: في الأساس، استبدلنا 3 ثم 2 في التعبير وحصلنا على الفرق بينهما.

هذه هي القيمة المحددة بدلا من استخدام

C

ثابتة في وقت سابق.

دعونا نستكشف العامل الثابت (فيما يتعلق بالتكامل غير المحدود) بمزيد من التفصيل. y 3

3y 2 ^{، ثم} 3 3y ² دي = y

3 ومع ذلك، ^3y 2 ^{يمكن أن يكون الفرق بين العديد من التعبيرات التي تشمل}

y 3 ^-5 ، > y 3 ⁺⁷ ، الخ … وهذا يعني أن الانعكاس ليس فريدا لأن الثابت غير معروف خلال العملية. بشكل عام 3y ² هو الفرق y

3 + C ^حيث C هو ثابت. وبالمناسبة، يعرف C باسم ^{"ثابت التكامل"} . نكتب هذا على النحو التالي: ∫ 3y 2. دكس = y

3

+ C ^{تقنيات التكامل من أجل التكامل غير المحدود، مثل بحث الجدول أو التكامل ريشش، يمكن أن تضيف انقطاعات جديدة أثناء عملية التكامل. تظهر هذه الانقطاعات الجديدة لأن المضادات المشتقة يمكن أن تتطلب إدخال لوغاريتمات معقدة.} لوغاريتمات معقدة لها انقطاع القفز عندما تقاطع الوسيطة المحور الحقيقي السلبي، وخوارزميات التكامل أحيانا لا يمكن العثور على تمثيل حيث هذه القفزات إلغاء.

إذا تم تقييم التكامل المحدد من خلال حساب أولا جزءا لا يتجزأ من التكامل ثم استبدال حدود التكامل في النتيجة، يجب أن ندرك أن التكامل غير المحدود قد ينتج انقطاعات. إذا فعل ذلك، بالإضافة إلى ذلك، يجب علينا التحقيق في الانقطاعات في فترة التكامل.